What would I say if someone should ask me to tell him/her to explain in ten words what relativity means. First of all I would think real hard. It's not so easy for a first year student to say in ten words what the subject is about. But I would try. This is what I would say about relativity: "Dealing with movement from different perspectives". What did I just say? Sometimes it's just hard to say something in so little words. I'll start with relativity in the classic way, like Galilei and especially Newton saw them.

Relativity is about comparing two things. If you have two apples, you can say that one apple is redder than the other one, you compare them. This is sort of the basic idea of relativity.

Now let's take another example, this time with two cars. These cars move in the same direction with different speeds. Now you notice that one car moves faster than the other car. THAT is relativity. With relativity you can now calculate how much faster one car is than the other. This is easy to do, the answer is just to subtract one speed by the other. If the cars go in opposite directions, you have to cast up the speeds to get the answer.

Õ

Example 1:

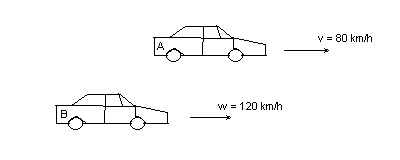
In this example you have two cars, A and B. Car A is driving wit a speed v, which is 80 km/h. Car B is driving with a speed w, which is 120 km/h. Now say that car B is 1 km behind car A, what time would it take for car B to catch up car A?

Answer:

The relativity principle says that you can look the whole situation from one of the cars, or with other words that you can move with one of the cars. Let us move along car A. By going at the same speed as car A, it looks like car A stands still. It has gone back from 80 to 0. Because of the new perspective you have to adjust the speed of car B too, by also reducing it with 80, which gives you 40 (120-80). This is the hard way of saying that must take the difference between the speed of car A and B; w - v = 120 - 80 = 40 km/h. Now you have reduced the speed of car A to zero and the speed of car B to 40.

So if you would draw a picture of the reduced situation (which seems like a reduced situation because of the perspective), this is how it would look like:

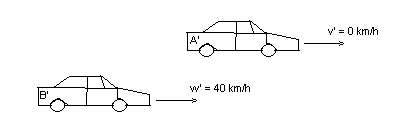
In this situation car B approaches car A, which seems to stands still, with a speed of 40 km/h. The answer in this situation is a piece of cake and is still the same as the original situation: How long will it take you to move along 1 km with a speed of 40 km/h? Since speed is distance divided by time, you can get the time by dividing distance by speed. This will give you 1/40 = 0,0025 hours. Multiply by 60 (one hour has 60 minutes) will give 1,5 minutes. Multiply by another 60 (a minute has 60 seconds) will give you 90 seconds.

It takes 90 seconds for car B to catch up car A.

 Õ

Here is another example of the same problem. Now the cars move in opposite direction.

Õ

Example 2:

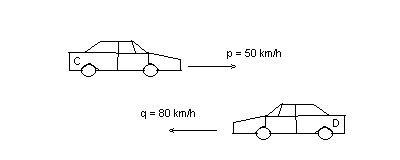
Here we are going to solve the same problem as in example one, but this one is slightly different. Again two cars, this time we'll call them C and D. Car C has a speed p, which is 50 km/h. Car D has speed q, which is 80 km/h, but in the opposite direction of car C. Car D is nearing car C, the distance is again 1 km. How long will it take before the cars meet?

Answer:

We again reduce the speeds of both cars by looking at the situation with the perspective of car C. Now you have to subtract 50 from car D's speed, but now you have to beware of the different directions. This means that car D has a speed of -80km/h. So you have to subtract 50 from -80, which gives you -130 km/h (the minus sign only gives the direction). Here too counts the difference between the two speeds: p - q = 50- (-80) = 50 + 80 = 130. It's very important in this case that you notice the different directions (this case is easy because the cars move in one line, but what if the two cars don't move in one line?). So this is how the new situation looks like:

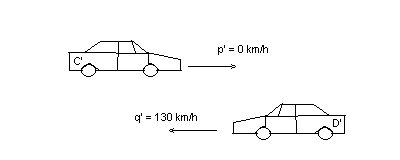
Sow how long does it takes to drive over a distance of 1 km with a speed of 130 km/h? Again you can use the equation that time is distance divided by speed: 1/130 = 0.0077 hours. This equals to 27.7 seconds.

Õ

Let's make things a little bit complicated. Assume that you sit in a car B (example 1). It looks like that you are standing still and that the other car is coming to you. At which speed you may ask your self. It's the same problem as example 1, but from a different perspective. Car A has a speed from your point of view that equals v - w=-80 - 120= -40 km/h (beware that the minus sign only speaks of the direction, in this case car A is travelling backwards for you so that's why the speed is negative). This is called a transformation.

Here I have illustrated the problem of different points of view. I might as well have chosen for sitting in a space shuttle and viewing the situation from there. The result would have been the same, no matter what speed the shuttle has, nor the cars have…well, this is not entirely true. What I've just discussed was the relativity principle as discussed by Galilei and Newton. This principle of watching the same thing from different points of view is essential. A point of view is called can be described as a co-ordinate system, or scientifically said an inertial system. In all inertial systems Newton's laws must be applicable. If this were not the case, the transformations would not give the same answer.

In this principle there's a problem. Let me illustrate the problem with an example.

Õ

Example 3:

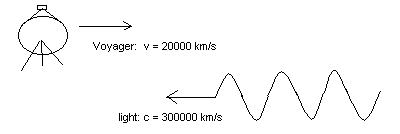
Question: At which speed does the satellite Voyager encounter the light particle (assuming it's a particle)?

Õ

Examining the previous examples you would say that the answer is about 320000 km/s (kilometres per second). Let me tell you this, this is all wrong. Maybe in the future we will be able to exceed light-speed, but with the conventional methods we will never do that. The light-speed, 300000 km/s, is the upper boundary for all speeds, you will not exceed that. At least, if we are to believe someone called James Clerk Maxwell. According to his theory (Electrodynamics), the light-speed is a constant, independent of the speed you have. This is in conflict with the Galileian transformations I've presented to you. Does this mean that this whole thing with Galilei and Newton is wrong? Yes and no. If you are very strict, you won't use the Galileian transformation, but then again, when dealing with common life situations, you won't notice any effect of this phenomenon due to the very small speeds.

So now it becomes time to suite the Galileian transformations for electrodynamics. This means that when you measure the speed of light from different systems, you must get the same result from every measurement you do: 300000 km/s.

The special theory of relativity gives you the methods of dealing with these kinds of situations.